Polynomial Division Over Finite Field
A monic irreducible polynomial of degree n having coefficients in the finite field GF q where q p t for some prime p and positive integer t is called a primitive polynomial if all of its. Nussbaumer polynomial transforms 42 43 constitute yet another essential tool for our new results.
Divide by in the Galois field GF 3 three times.
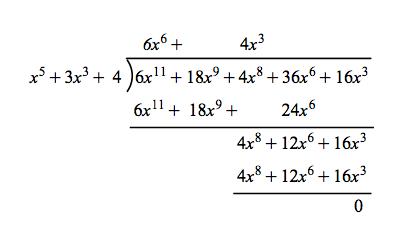
Polynomial division over finite field. G x2 - 17 sage. In a similar way as in SchönhageStrassens second algorithm from 49 the idea is to use DFTs over a ring with. However the vertical spacing between each line and exponents of the equation below it is quite small how to increase it.
For example all polynomials are over GF 3. F x3 1. Q_rvr_rv gfdeconv bap q_rv 14 1 0 0 1.
Lets say we want to divide 5x2 4x 6 by 2x 1. The polynomial P x4 1 is irreducible over Q but not over any finite field. The elements of F x are called polynomials over F.
The polynomial r x is called the remainder of f x modulo g x. X 3 x 2 1 and x 3 x 1. A 1 1.
Addition is equivalent to taking the XOR of. B 0 1 0 1 1. I attempted the following solution.
Now your mental gymnastics must include both additive inverses and multiplicative inverses. Theorem 1 The Division Algorithm for Polynomials over a Field. X QQx0 sage.
H x3 1 x2 - 17 sage. Polynomial ring rm Fx for rm F a field as above. For example to construct the finite field GF2 3 we need to choose an irre- ducible polynomial of degree 3.
Fx x - alphaqx beta beta in mathbb F_pn Inserting x alpha in the above equation proves beta 0 and f x - alphaq contradicting irreducibility. Consider again the polynomials defined over GF7. In particular these results are studied when one studies normal forms for finitely-generated modules over a PID eg.
There are only two such polynomials. Hparent Fraction Field of. On every other finite field at least one of 1 2 and 2 is a square because the product of two non-squares is a square and so we have If.
The degree of a polynomial is the highest power of variable in it. Let F cdot be a field and let f g in Fx with gx neq 0. Represent the polynomials using row vectors and divide them in GF 3.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. A polynomial f x of positive degree is said to be reducible over F if there e xist two polynomials g x and h x over F such that 1 deg g x deg h x deg f. When one studies linear systems of equations with coefficients in the non-field.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. We carry out division with remainder dividing f by the polynomial x - alpha. In particular Theorem 12 implies that a DFT of length over a finite field can be computed in time on a Turing machine.
For polynomials a x b x and g x which are over the same field we say a x is congruent to b x modulo g x written a x b x mod g x if m x divides a x - b x. Cite PARI in your work as well. A polynomial m x is called irreducible if and only if m x cannot be expressed as a product of two poly- nomials both of degree lower than that of m x.
Self-reciprocal polynomials over finite fields are used to generate reversible codes with a read-backward property J. Dividing polynomials defined over a finite field is a little bit more frustrating than performing other arithmetic operations on such polynomials. Dividing two polynomials constructs an element of the fraction field which Sage creates automatically.
Is there a package like polynom for typesetting polynomial long division but over a finite field such as GF2. Represent the polynomials as row vectors character vectors and strings. On any field extension of F2 P x 1 4.
Then there exists unique q r in Fx such that fx gxqx rx with the property that either rx 0 or degr degg. If not how to manually typeset long division in general. There are many irreducible polynomials sometimes called reducing polynomials that can be used to generate a finite field but they do not all give rise to the same representation of the field.
Extended polynomial GCD in finite field The calculator computes extended greatest common divisor for two polynomials in finite field.
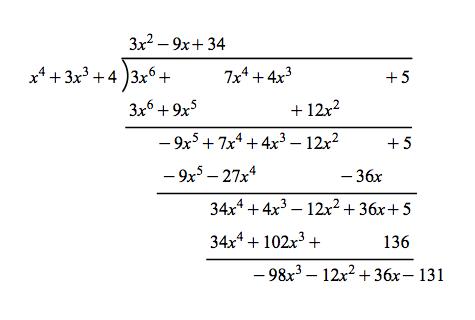
Galois Theorem And Polynomial Arithmetic

Finding The Greatest Common Divisor Of Polynomials Over A Finite Field Youtube

Mathematical Background Extension Fields Ppt Download

Polynomial Long Division Over Gf P Tex Latex Stack Exchange

Division In Finite Fields Mathematics Stack Exchange
Addition And Multiplication In A Galois Field Mathematics Stack Exchange
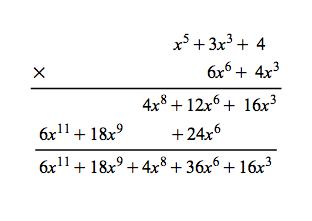
Galois Theorem And Polynomial Arithmetic

Polynomial Long Division Over Gf P Tex Latex Stack Exchange
Finite Fields Of The Form Gf 2n
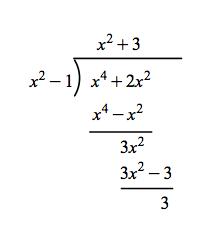
Galois Theorem And Polynomial Arithmetic

Section 4 5 Polynomial Arithmetic Cryptography And Network Security 4th Edition

Addition And Multiplication In F 4 Mathematics Stack Exchange

Performing Division And Multiplication Over Gf P Mathematics Stack Exchange
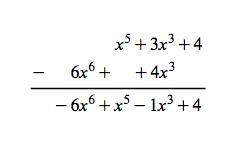
Galois Theorem And Polynomial Arithmetic
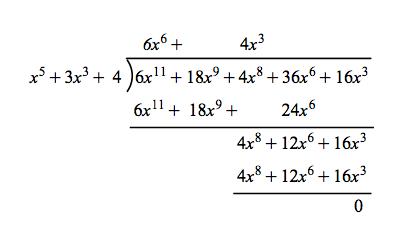
Galois Theorem And Polynomial Arithmetic
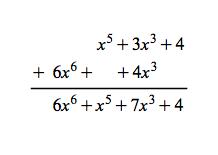
Galois Theorem And Polynomial Arithmetic

Finding The Gcd Of Two Polynomials Over A Finite Field Youtube